This post is the follow-up of the previous one explaining the algorithms. In this one, we will see how we can get more interesting generations.

Note : Have a look at the original github repository implementing this algorithm.

Handling symetry for efficient generation

So far, we had to define manually the adjacency matrix. This is not something that ones wants when the number of blocks increase. It is also very tedious if not impossible to do it manually without a general rule.

This can be easily applied to domino-like tiles. They need a matching number in order to be connected together.

Symmetry rules are defined on top of connected-or-not rules between tiles.
To simplify our example, we will keep only 1-0 connections
 
     up right down left 
T =  [0   1.    1.   1.]

We can deduce connectivity of rotated version of T

       up right down left 
- T  = [0   1.    1.   1. ]
- |- = [1   1.    1.   0. ] rotated right once 90° 
- | =  [1   1.    0.   1. ] rotated right twice 90° 
- -| = [1   0.    1.   1. ] rotated right thrice 90° 


To find connections between symmetric transformation of peices we can use the following rule building : 

 - Right connection T and |-  == M[0, right] * M[1, left]

We need to build two functions :

• One to create the different rotations of a single tile
• Building the adjacency matrix based on the connectivity vectors of all tiles

All rotations finctions

T_CONNECTIVITY = [0, 1, 1, 1]
ROT_90_MAT = np.array([[0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1], [1, 0, 0, 0]])

def build_all_rotations(ref_pieces):
    assert type(ref_pieces) == list
    result_array = []
    for ref_piece in ref_pieces:
        result_array.append(ref_piece)
        for _ in range(3):
            result = ROT_90_MAT.dot(result_array[-1])
            result_array.append(result)
    return result_array

build_all_rotations([np.array(T_CONNECTIVITY)])

#>>[array([0, 1, 1, 1]),
#   array([1, 1, 1, 0]),
#   array([1, 1, 0, 1]),
#   array([1, 0, 1, 1])]

In this block, we define the connectivity vector of a T shaped tile :

• Up : NO
• Right : YES
• Bottom : YES
• Left : YES

In fact, to tile can connect if they have the same symbol, so a NO-NO connection is possible.

Now the rotation, with a 90-degree rotation, we can update the original vector to get the connection info of the rotated tile. 90 deg rotated T :

• Up : YES
• Right : YES
• Bottom : YES
• Left : NO

That’s it, we have created new tiles by symmetry.

Building the adjacency matrix

Now we create the part defined as adj(rigth, 0, 1) == M[0, right] * M[1, left]

direction_dictionnary = {
    3: (-1, 0), 0: (-1, 0), 1: (0, 1), 3: (0, -1)
}

def build_adj_from_number_vec(vector_array):
    N = len(vector_array)
    adj = {direction: np.zeros((N, N)) for direction in direction_dictionnary.values()}
    for direction_index, direction in direction_dictionnary.items():
        for i in range(N):
            for j in range(N):
                adj[direction][i, j] = vector_array[i, direction_index] == vector_array[j, (direction_index + 2) % 4] 
    return adj
    
    
adj = build_adj_from_number_vec(np.array(build_all_rotations(np.array(T_CONNECTIVITY))))

The formula is just retranscribed with adj[direction][i, j] = vector_array[i, direction_index] == vector_array[j, (direction_index + 2) % 4] We just need to iterate over all triples (direction, i, j). It’s important to do them all because even i-i interaction are meaningful

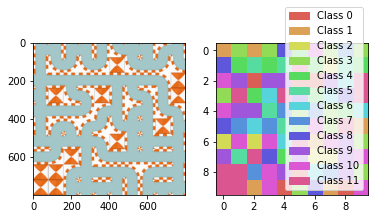
Some generations

Generated with T shaped pipes only

Generated with T and L shaped pipes

Generated with all possible shapes