Wave function collapse part 1
This is a post presenting how I reimplemented the Wave function collapse presented in this github repository
The Algorithm
An example
Let’s start with an example of what the algorithm can do. On a grid, 3 colors are possible for each position but two neighbours cannot have the same color. Now fill the grid and respect this rule.
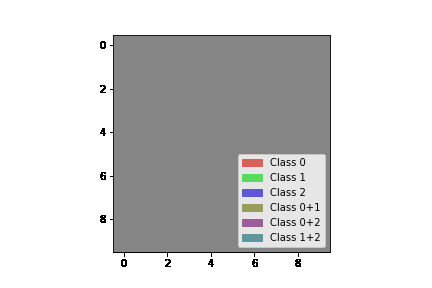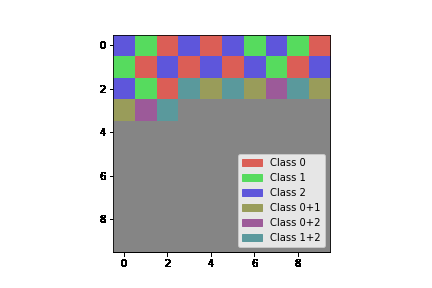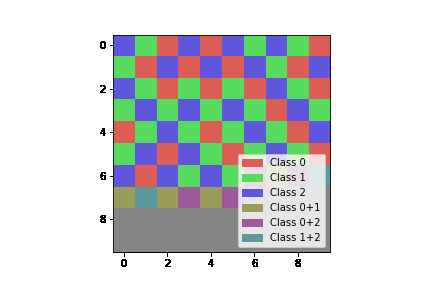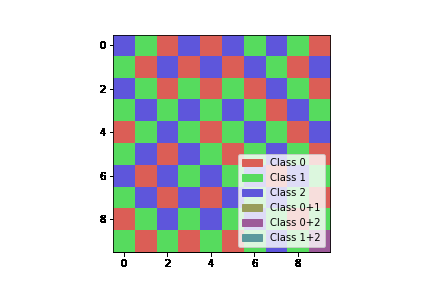
This execution is what you could have done by doing it manually. The wave function collapse algorithm allows to implement this filling for that kind of constraint and many others
The steps
The algorithms contains two main steps.
- Collapse : choose a state on a position with minimal entropy (= minimal remaining options)
- Propagate the constraint of the new choice on the whole grid
These two steps are repeated until all positions on the grid have a given state / color My implementation in python can be found in this notebook
Code for each phase
How data is organized : the map and the adjacency matrix
The state map
wave = np.ones((3, 10, 10)) # 3 possible state, 10x10 map
# Force position 0,0 to class 3
wave[:, 0, 0] = 0
wave[2, 0, 0] = 1
The adjacency matrix
# All classes have the same pattern :
# The same class is not tolerated in the direct neighboorhood
# All adj[i, i] = 0, all other adj[i, j] = 1 if i!=j
prop_base = np.array(
[[0, 1, 1],
[1, 0, 1],
[1, 1, 0],
]
)
# Here for all direction we assign the same neighboorhood rule
# The tuple used as key defined the direction (y, x)
adj = {(-1, 0): prop_base, (1, 0): prop_base, (0, -1): prop_base, (0, 1): prop_base}
Selecting a state
At every round of the algorithm, we will make a decision to collapse a state to a single class.
[0, 1, 1] may become [0, 0, 1]
def select_location(wave):
# We want to find location of low entropy (state almost defined)
# We replace location already collapsed with high values to be sure to find location
# that are still not collapsed but with the lowest possible entropy
sub_index = np.where(np.sum(wave, axis=0) > 1, np.sum(wave, axis=0), 10000)
# Find lowest loc
index = np.argmin(sub_index)
i = int(index / wave.shape[2])
j = index % wave.shape[2]
return i, j
Here we just find a location. We need to select at random a state for this tile.
This could be done differently when ties are present to enforce other properties like a certain distribution of tiles.
Propagation algorithm Now the core algorithm, how the contraint is propagated accross the whole matrix.
Per element the formula is the following
wave[:, i + di, j + dj] *= wave[:, i, j] * adj[(di, dj)]
[d] *= [d] * [d x d]
It can be vectorized with :
wave[:, u + du] *= wave[:, u] * adj[du]
[d] *= [d] * [d x d]
wave'[:, : + du].t *= adj[u] * wave[:, :]
[N x d] *= [Nxd] * [d x d]
In python, this looks like this :
def one_iter_propagate(wave, adj):
# Create a padded version of the map, so we can take a whole slice
padded = np.pad(
wave, ((0, 0), (1, 1), (1, 1)), mode="constant", constant_values=True
)
# To gather the update over the 4 directions
update = dict()
for d in adj:
dx, dy = d
# We take a different crop depending on the direction
current = padded[
:, (dx + 1):(wave.shape[1] + dx + 1), (dy + 1):(wave.shape[2] + dy + 1)
]
# We compute the constraint of direction-neighbour on the current element in a vectorized fashion
update[d] = (adj[d] @ current.reshape(current.shape[0], -1)).reshape(current.shape)
# Finally the computed constraint are applied on the current position
# new_state = [1, 0, 0] = old_state = [1, 0, 1] * [1, 0, 0] neigbour_constraint
for d in adj:
wave *= update[d]
np.clip(wave, 0, 1, out=wave)
This code is the direct application of the vectorized formula presented a few line before.
All in one
All the different parts of the algorithms are combined in this single class
class WFC:
class ContradictionException(Exception):
pass
@classmethod
def one_iter_propagate(cls, wave, adj):
padded = np.pad(
wave, ((0, 0), (1, 1), (1, 1)), mode="constant", constant_values=True
)
update = dict()
for d in adj:
dx, dy = d
current = padded[
:, (dx + 1):(wave.shape[1] + dx + 1), (dy + 1):(wave.shape[2] + dy + 1)
]
update[d] = (adj[d] @ current.reshape(current.shape[0], -1)).reshape(current.shape)
for d in adj:
wave *= update[d]
np.clip(wave, 0, 1, out=wave)
@classmethod
def propagate(cls, wave, adj):
count = 0
last_count = 0
while last_count != wave.sum():
last_count = wave.sum()
cls.one_iter_propagate(wave, adj)
if (wave.sum(axis=0) == 0).any():
raise cls.ContradictionException("Contradiction found")
count += 1
return count
@classmethod
def select_location(cls, wave):
sub_index = np.where(np.sum(wave, axis=0) > 1, np.sum(wave, axis=0), 10000)
index = np.argmin(sub_index)
i = int(index / wave.shape[2])
j = index % wave.shape[2]
return i, j
@classmethod
def choose_state(cls, wave, u, v):
array = wave[:, u, v]
indices = list(range(array.shape[0]))
norm_array = array / sum(array)
state_chosen = np.random.choice(indices, p=norm_array)
wave[:, u, v] = 0
wave[state_chosen, u, v] = 1
return state_chosen
@classmethod
def wave_collapse_agorithm(cls, wave, adj):
iteration = 0
wave_array = list()
while wave.sum() > wave.shape[1] * wave.shape[2]:
# We save the previous wave state in case of error
wave_array.append(wave)
u, v = cls.select_location(wave)
state_chosen = cls.choose_state(wave, u, v)
try:
cls.propagate(wave, adj)
except cls.ContradictionException:
# Recover previous state
wave = wave_array.pop()
# Set the option previously taken as impossible
wave[state_chosen, u, v] = 0
iteration += 1
if iteration > 100 * wave.shape[1] * wave.shape[2]:
break
@classmethod
def run_wave_collapse(cls, my_adj, h, w):
n_tiles = my_adj[(-1, 0)].shape[0]
wave = np.ones((n_tiles, h, w))
# Run the wave collapse alg
cls.wave_collapse_agorithm(wave, my_adj)
return wave
Some generations
Now let’s see what we can get with this algorithm.
Basic map with classes display
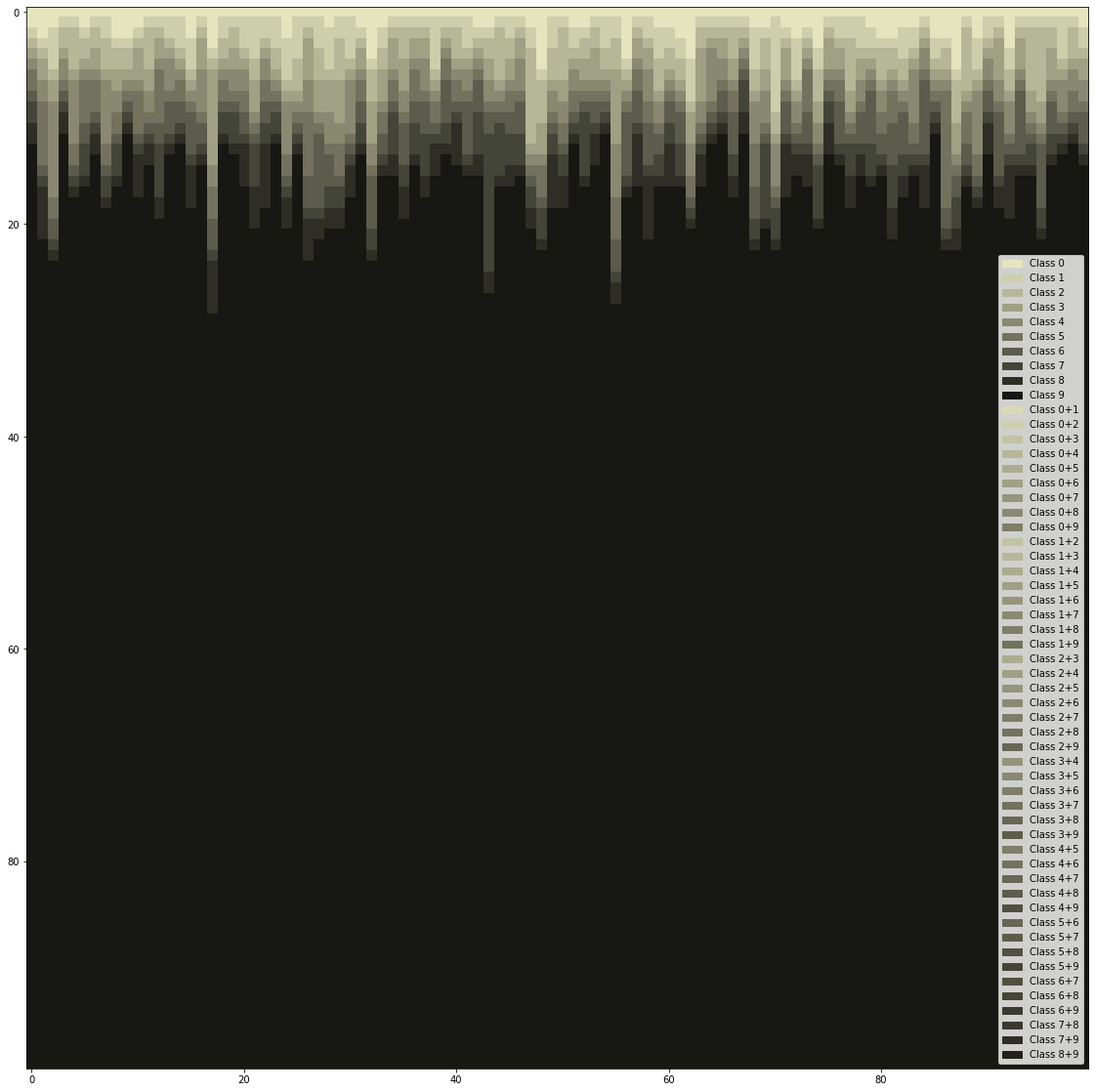Generated using vertical dependencies : classes ranges from 0 to 9.
0 is necessarily at the top of the screen. Vertical neighbours of class i are necessarily class i or i + 1