I collected a number of code samples to plot graphs. All of them needed me to google a few things and dive into the matplotlib documentation. So it is usually a good starting point when you start a new analysis.

We will see three examples

A cumulative distribution
A count plot
A frequency plot

The cumulative distribution with hist

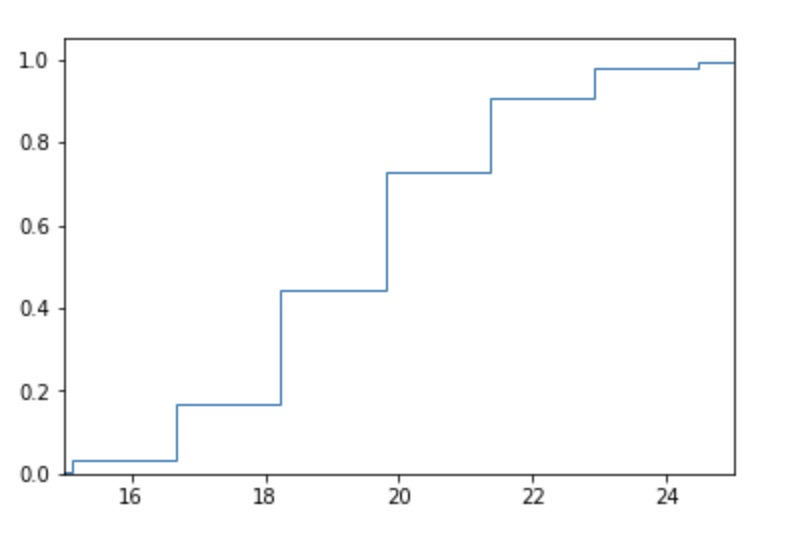
cumulative distribution

Easy enough with hist. However it is often

fig, ax = plt.subplots()
data = [np.random.lognormal(3, 0.1) for _ in range(10000)] 

max_val = int(np.quantile(data, 0.99))
min_val = int(np.quantile(data, 0.01))

ax.hist(data, None, histtype='step', cumulative=True, density=True)

ax.set_xlim(min_val, max_val)

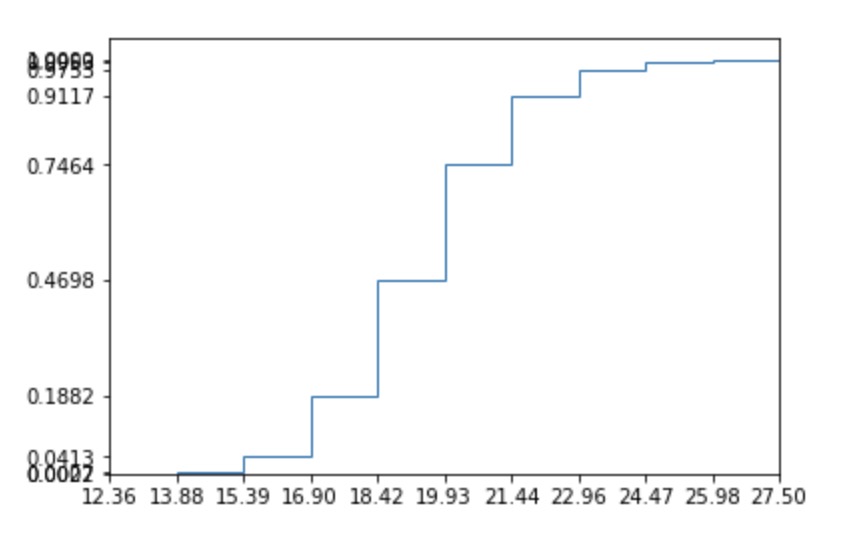
You can pimp a little bit your histogram to be able to read the probabilities. We can just change the last lines to have :

prob, buckets, _ = ax.hist(data, None, histtype='step', cumulative=True, density=True)

ax.set_xlim(min_val, max_val)
ax.set_xticks(buckets)
ax.set_yticks(prob)

cumulative distribution

Plot the most frequent terms from an array

Seaborn has an built-in function, but we can do a little bit better without much effort.
Note that it is relatively painful to change the plot options with the seaborn way.

import seaborn as sns
from collections import Counter


# Generate the data
choices = ["Poney", "Cat", "Dog", "Insect", "Bug", "Turtle", "Guinea pig", 
           "Pig", "Horse", "Lion", "Dragon", "Unicorn", "Elephant", "Others", "Kangoroo", 
           "Koala", "Dolphin", "Shark", "Rat", "Cockroach", "Beatle", "Gull", "Crow", "Eagle"]
prob = np.array([np.random.random() for _ in range(len(choices))])
prob /= sum(prob)
data = [np.random.choice(choices, p=prob) for _ in range(10000)] 

# Seaborn Countplot
fig, ax = plt.subplots()
sns.countplot(data)
ax = plt.gca()
labels = [t.get_text() for t in ax.get_xticklabels()]
plt.xticks(range(len(choices)), labels, rotation="vertical", fontsize=10)


# Custom Countplot
def plot_count(data,  title="", counted=False):
    
    plt.style.use("seaborn")
    
    if not counted:
        counter = Counter(data)
    else:
        counter = data
    
    fig, ax = plt.subplots()
    size = 10
    most_common = counter.most_common(20)
    
    for i, l in enumerate(most_common):
        rects1 = ax.bar(size * i, l[1], size / 1.5, label=str(l[0]))
    
    labels = [most_common[i][0] for i in range(len(most_common))]
    ticks = [size * i for i in range(len(most_common))]
    ax.set_title(title)
    plt.xticks(ticks, labels, rotation="vertical", fontsize=10)
    
    
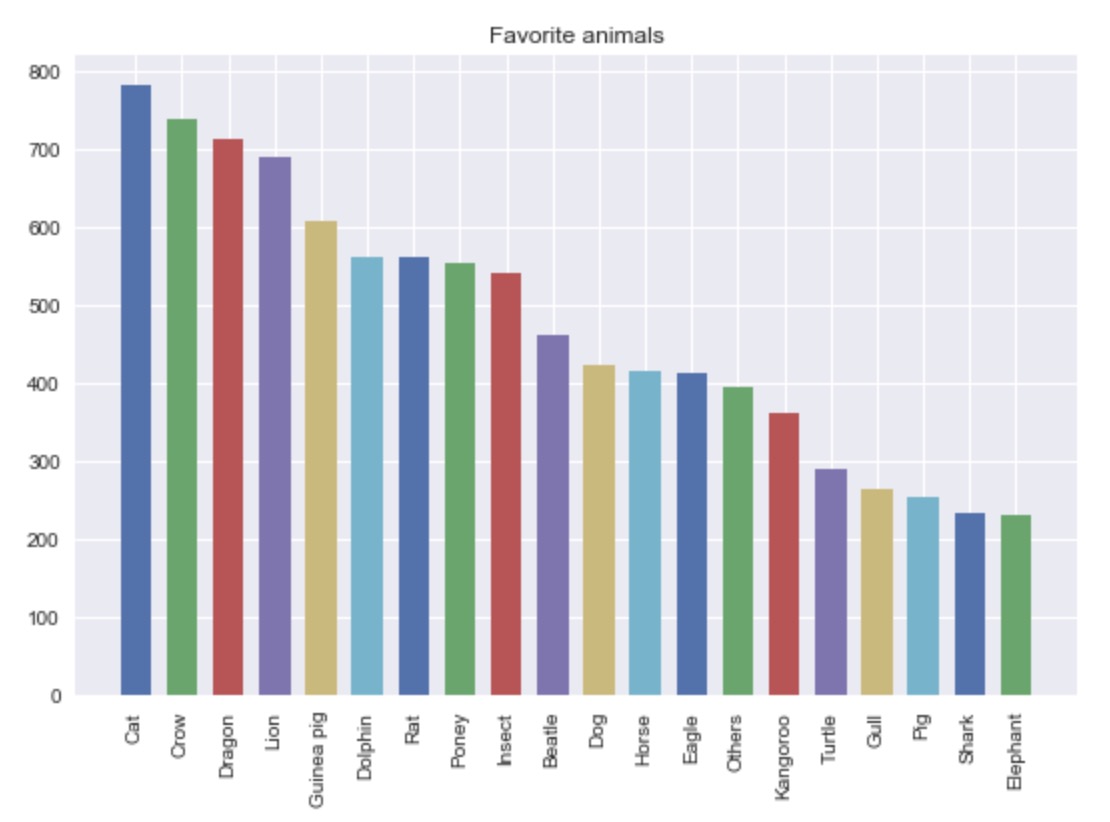
plot_count(data, "Favorite animals")

We get the following plots :

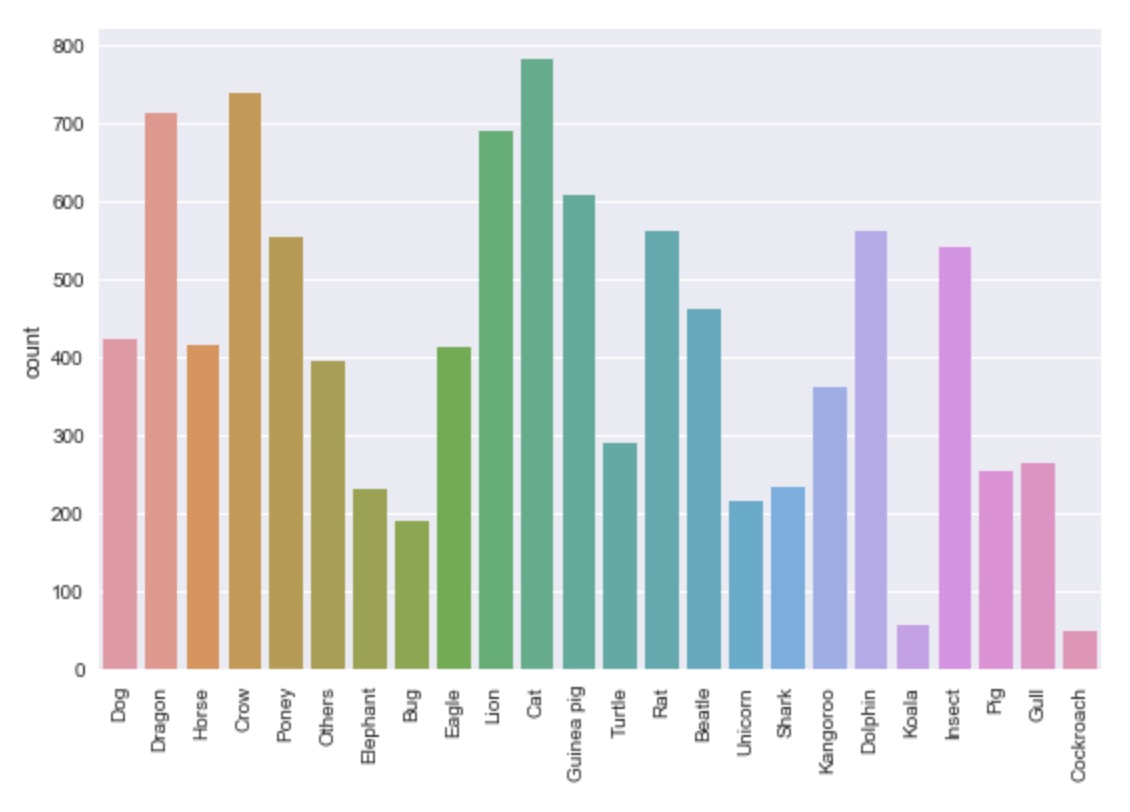different countplots 1 The Seaborn countplot

different countplots 2 And out custom countplot

With our custom plot, we can easily see which animal is everyone’s favorite ! This will be even more useful with our next example.

Plot relative frequencies

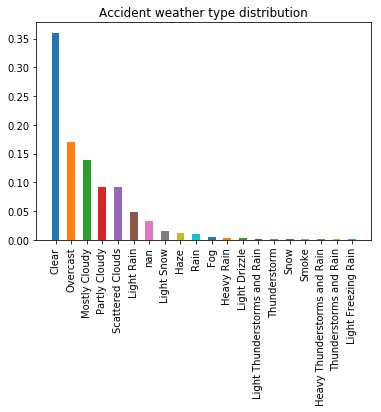
We will use data from the US accident dataset.

import pandas as pd
df = pd.read_csv("/Users/a.morvan/Downloads/US_Accidents_May19.csv")
data = df["Weather_Condition"].values
counter = Counter(data)
c_normalised = Counter({k: v / total_count 
                        for k, v in counter.items()})
plot_count(c_normalised, 
           "Accident weather type distribution", 
           counted=True)

My plot count

Now let’s have a look at the difference when the accident is on a roundabout.

# Collect roundabout accident only weather conditions
df_roundabout = df[df["Roundabout"] == True]
data = df_roundabout["Weather_Condition"].values

# Apply the count 
roundabout_weather_counter = Counter(data)
total_roundabout = sum(roundabout_weather_counter.values())
# Difference : remove the global avergae on each category !!!
center_normalised_roundabout_weather_counter = \
    Counter({k: (v / total_roundabout) - c_normalised[k] 
             for k, v in roundabout_weather_counter.items()})

plot_count(center_normalised_roundabout_weather_counter, 
           "Accident weather type distribution on roundabouts", 
           counted=True)

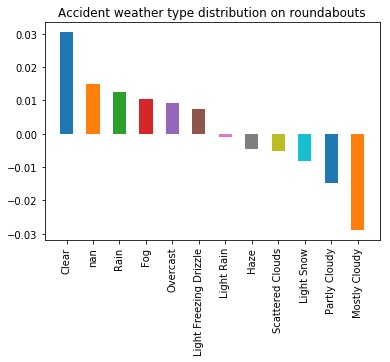
My plot count for subgroup

This is a great way to find variables that can be predictive of a particular event.