Can i boost anything?
What is boosting ?
What is boosting ? It is the idea to use a combination of “weak” classifiers instead of a strong single one and get better performances.
[F(x) = \Sigma_m \gamma_m F_m(x)]
F is built iteratively by adding at each iteration a function \(\gamma_m F_m(x)\) that will feat an altered version of the training set (X, Y).
Boosting has been made famous with GDBT (implemented in the XGBoost lib). However we are going to see a simpler method : Ada Boost. Ada Boost also had some glory in the past with the Viola-Jones detector that used a Haar cascade to detect faces in black and white img.
In this post, our objective will be to feat an arbitrary distribution of random varibale that have 0/1 realisation, we will know the true distribution and sample a set of points \((x, y \in [0, 1])\). More over, we will do this with sclaed logistic regression unlike most of other approaches.
The base function : scaled logistic regression
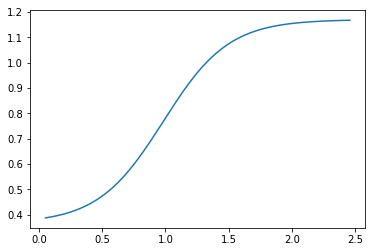
We are going to work with scaled logistic regression to allow a bit more modeling power. Here is an example of implementation
import torch
import torch.nn.functional as F
class LogisticRegression(torch.nn.Module):
def __init__(self, a):
super(LogisticRegression, self).__init__()
self.linear = torch.nn.Linear(1, 1)
self.a = torch.nn.Parameter(a * torch.ones(1), requires_grad=True)
# parameter used for the ada boost weighting between models
self.w = torch.ones(1)
def forward(self, x):
y_pred = self.a * F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegression(1.180)
Let’s have a look at the shape of the function.
The base training procedure
For information, we train the logistic regression model with Adam using the full dataset as it is very small.
cap = lambda X: torch.min(torch.ones(X.shape[0]), torch.max(torch.zeros(X.shape[0]), X))
total_pred = lambda models, X: cap(sum([m.w * m(X)[:, 0] for m in models]))
def train_(models, model_, X, Y, X_importance=None):
if X_importance is None:
X_importance = (1. / X.shape[0]) * torch.ones(X.shape[0])
else:
X_importance = torch.tensor(weights)
def routine(optimizer):
for epoch in range(1000):
model_.train()
optimizer.zero_grad()
# Forward pass
Y_pred = total_pred(models + [model_], X)
# Compute Loss
loss = F.binary_cross_entropy(Y_pred, Y, weight=X.shape[0] * X_importance)
# Backward pass
if epoch % 500 == 0:
print(loss)
loss.backward()
optimizer.step()
routine(torch.optim.Adam(model_.parameters(), lr=0.05))
routine(torch.optim.Adam(model_.parameters(), lr=0.01))
The algorithm
Now let’s see how Ada Boost works. The algorithm has many variants, but we will use a simple version.
AdaBoost maintains a score per sample that correspond to its difficulty so far. The difficulty correspond to how much the sample is misclassified. Each time we add a new model to the ensemble, we try to reduce the error of the ensemble weighted by the difficulty.
[\epsilon_m = \Sigma_i D_m(i)[y_i \neq F(x_i)]]
We will add the model Fm learned on this round to the ensemble with a coefficient based on this error.
Summary
- Bagging : select N_sample / 2 element of the training set using sample with replacement using the weights as probability distribution
- Train the model m by minimizing the loss of the ensemble on the training set selected before
- Compute performance to find the coefficient with which the model model will be added to the ensemble
- Update the weights based on the latest performance of the model
Now, let’s have a look at the implementation :
def ref_ada_boost(models, X, Y, weights=None):
"""
models: List[ScaledLogisticRegression]
X : torch tensor of shape [N, 1]
Y : torch tensor of shape [N]
weights: difficulty weight of size N
"""
# 0 : some sanity check
if weights is None:
weights = (1. / X.shape[0]) * torch.ones(X.shape[0])
else:
weights = torch.tensor(weights)
# 1. Bagging step, we sample from the dataset around half of the total size, we sample based on the difficulty
sampling = np.random.choice(list(range(X.shape[0])), int(0.5 * X.shape[0]), p=weights.numpy())
X_sampled = X[sampling]
Y_sampled = Y[sampling]
# 2. model training
model_ = LogisticRegression(1.0)
train_(models, model_, X_sampled, Y_sampled)
# 3. computation of performance
total_prediction = total_pred(models + [model_], X)
print("Training finished with loss : {}".format(F.binary_cross_entropy(total_prediction, Y)))
pre_prediction = total_pred([model_], X)
prediction = (pre_prediction >= 0.5).float()
label_correctness = (prediction == Y).float()
non_agg = weights * label_correctness
e = torch.sum(non_agg)
print("e = {}".format(e))
# Early exit if the model doesn't do better than randomness
if e < 0.5:
return None
# 3 - we compute the w to add model_ to the ensemble (models), it depends on the error of the model
# Small change on the w formula, we use the correct elements instead
model_.w = 0.5 * torch.log(e / (1 - e))
print("w for this model", model_.w)
# 4 - the recompute the weights based on performances
sigma = 2 * (e * (1-e)) ** 0.5
print("sigma", sigma)
for i, index in enumerate(set(sampling)):
weights[index] *= torch.exp(-model_.w * (1.0 if label_correctness[i] > 0 else -1.0)) / sigma
weights /= torch.sum(weights)
models.append(model_)
return weights
my_models = list()
weights = ref_ada_boost(my_models, X, Y)
# Multiple rounds are needed to feat correctly the curve
for _ in range(10):
assigned_weights = ref_ada_boost(my_models, X, Y, weights)
if assigned_weights is None:
break
else:
weights = assigned_weights
Experiments
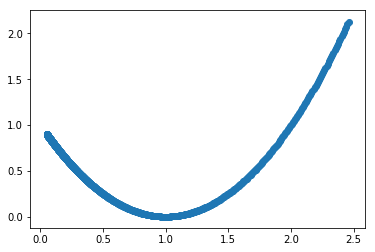
Feating a parabolic curve with logistic regressions
import numpy as np
import random
# The true probability distribution (values above 1 count as 1)
g = lambda x: (x - 1) ** 2
# sampling process, given the probability from g(x) we get a 0 or a 1
f = lambda x: 1 if random.random() < g(x) else 0
# We sample a thousand points from the process described above
x = np.array(list(map(lambda x: np.exp(x), np.linspace(-3, 0.9, 1000))))
y = list(map(f, x))
# Data used for the logistic regression
X = torch.FloatTensor(np.array(x).reshape(-1, 1))
Y = torch.FloatTensor(np.array(y))
# The plot of the distribution
plt.scatter(x, g(x))
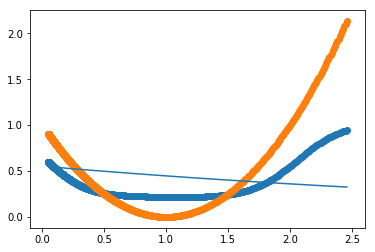
Boosting of logistic regression
We run this boosting procedure on the described U shape.
complete_prediction = sum([m.w * m(X) for m in my_new_models])
complete_prediction = torch.min(torch.ones(complete_prediction.shape), torch.max(torch.zeros(complete_prediction.shape),complete_prediction))
plt.scatter(x, complete_prediction.detach().numpy())
plt.scatter(x, g(x))
Y_pred = my_new_models[0](X).detach().numpy().flatten()
plt.plot(x, Y_pred)
We can observe the original curve, the boosted model in thick and the first learned model in thin.
Conclusion
We have seen that Ada Boost can provide some modeling power even if the function used for the boosting is not a decision tree. Let’s conclude with this list of pros and cons.
Pros
- Feat arbitrary shape with function that have limited modeling power
- Almost no change to the training procedure of the original model –> easy to add to any system
Cons
- The methods is threshold based, >0.5 means 1 in term of classification. This should be adapted for efficiently handling probability distributions.
- Prediction costs increases rapidly (fortunately logistic regression is very simple, thus fast enough)